Zachowanie się wirnika podatnego giętnie podczas ruchu obrotowego

Jak postępujemy z wirnikami podatnymi giętnie?

Postępujemy w sposób różniący się zdecydowanie od postępowania z wirnikami sztywnymi. Po pierwsze zakładamy, że punkty podparcia wirnika nie są podatne. To oznacza, że przyjmujemy brak ugięcia w tych miejscach.

Po drugie wszelkie pomiary wykonujemy wzdłuż długości wirnika.

W zależności od wyboru metody wyważania obserwujemy sygnały pochodzące od sumarycznych ugięć, przy wybranej prędkości obrotowej, lub sygnały odpowiadające czystym postaciom własnym ugięć, przy kolejnych prędkościach krytycznych.

Niewyważenie wirników podatnych giętnie może składać się z tych samych składników, które są zawarte w niewyważeniu wirników sztywnych, ale zawsze dodatkowo składa się z niewyważenia wynikającego z ugięcia czyli odejścia masy wirnika od rzeczywistej osi wirowania. Właśnie to oddalenie się środków masy poszczególnych odcinków wirnika od osi wirowania jest główną przyczyną zmian niewyważenia, które rejestrujemy przy zmianie prędkości obrotowej. Decyduje ono o zachowaniu się wirników w trakcie obrotów.

Ustalanie się tego składnika niewyważenia, po osiągnięciu założonej prędkości obrotowej, wymaga komentarza.

Na rysunku 1 pokazano specyficzne sposoby zachowania się dwóch wirników. Pierwszy sposób obrazuje postaci drgań sztywnego wirnika podpartego na podatnych podporach - od góry do dołu rysunku, w zależności od rosnącej prędkości obrotowej. Drugi, analogicznie, postaci ugięcia osi wirnika podatnego podpartego na sztywnych podporach.

Rys. 1.  Wirnik sztywny, po lewej, przyjmuje dwie postaci własne. Wirnik podatny giętnie, po prawej, może przyjąć nieskończenie (teoretycznie) wiele postaci ugięć. Na rysunku pokazano dwie pierwsze.

Wirnik jest podatny, gdy wraz ze zmianą prędkości obrotowej zmienia się jego niewyważenie. Oznacza to, że zmieniają się wartości obliczonych niewyważeń.

Na wstępie należy zauważyć, że odkształcenie  i odpowiadające mu obciążenie wirnika powstałym niewyważeniem mają ten sam przebieg wzdłuż jego długości. Np. gdy wirnik ugnie się tak, jak wirująca dziecięca skakanka, przyjmując kształt połowy sinusoidy, to odpowiadające temu odkształceniu obciążenie niewyważeniem ma ten sam przebieg, gdyż rośnie wprost proporcjonalnie do odległości elementarnego odcinka wirnika od osi wirowania. Rosnące ugięcie powoduje rosnące obciążenie. Rosnące obciążenie wywołuje, w odpowiedzi, większe ugięcie. Ten mechanizm działa aż do osiągnięcia równowagi pomiędzy dwiema sumami prac, które wykonują siły występujące na wirniku. Ugięcie, dla wybranej prędkości obrotowej, ustala się, gdy suma prac wykonanych przez siły bezwładności jest równa pracom wykonanym przez siły sprężystości w materiale wirnika.

Niewyważenia spowodowane ugięciem osi wirnika przyjmują duże wartości. Strzałki ugięcia nie są duże, ale zachodzi efekt sumowania jednostkowych niewyważeń z  poszczególnych odcinków wirnika. Jeżeli braki kołowosymetryczności wynikają np. z nadmiarowych mas mocowanych na powierzchni wirników, to zmiany prędkości nie zmieniają znacząco wartości takiego niewyważenia. Strzałki ugięcia są bowiem nieporównywalnie mniejsze od średnic tarczy lub wałków wirników. Przez to zmiana odległości nadmiarowej masy od osi wirowania jest praktycznie do pominięcia.

Dla pełniejszego zrozumienia zachowania się wirników na obrotach, przeanalizujmy ruch tarczy o masie M i środku ciężkości w punkcie c - znajdującym się w odległości e od środka geometrycznego. Tarcza zachowuje się jak element długiego, masowego wału. Wiedząc, jak zachowuje się tarcza, można, poprzez analogię, rozpoznać zachowanie się masowego, długiego wału. Tarcza jest zamocowana do bezmasowego wału o sztywności na zginanie EI, gdzie E  jest modułem Younga i I jest momentem bezwładności przekroju poprzecznego, liczonego względem osi prostopadłej do osi wirowania. Zachowanie się tarczy wskazuje, jak tworzą się poszczególne postaci własne ugięć.

Wał jest posadowiony pionowo dla uniknięcia działania siły ciężkości i w połowie długości wału, aby uniknąć działania momentu żyroskopowego, który wystąpiłby, gdyby tarcza była zamocowana poza środkiem długości.

Moment żyroskopowy wystąpiłby na skutek drgań tarczy występujących w płaszczyźnie zawierającej oś wirowania wału. Takie drgania można by obserwować w postaci drgającego cienia na ścianie, oświetlając lampą wirującą tarczę zamocowaną prostopadle, ale nie w środku długości wału. Na skutek ugięcia wału wystąpiłyby drgania tarczy.

Rys. 2. Schemat zamocowania wirującej masowej tarczy do bezmasowego wału podatnego na zginanie.

W ruchu wirującej tarczy, jak na rys. 2, najistotniejszymi cechami jej zachowania jest względny obrót wirnika, niezależnie od jego obrotów wokół osi wirowania, kończący się dodatkowym ruchem wynoszącym połowę pełnego obrotu (czyli kątem obrotu , dla częstości zdecydowanie przekraczającej częstość własną oraz ustalenie się, przy tej częstości, amplitudy ugięcia wału: równej mimośrodowości tarczy .

Rys. 3. Ruch precesyjny, prosty i synchroniczny tarczy.

Podstawowy ruch obrotowy pokazano na rysunku 3. Można zauważyć, jak tarcza wykonuje ruch precesji prostej i synchronicznej. To oznacza, że częstość wirowania ugiętego wału jest równa częstości wirowania tarczy  (co jest oczywiste) i że obie prędkości są skierowane w tę samą stronę (co także jest oczywiste). Dla wybranej prędkości punkt , wyszczególniony na wale, wiruje wraz z wałem. Przez to maksymalnie rozciągana, od ugięcia, tworząca walca wirnika (znajdująca się w punkcie ) jest niezmiennie rozciągana, a tworząca ściskana jest niezmiennie ściskana. Nie występują więc tutaj drgania.

Tworzące zmieniają się następująco, względem ugięcia, przy zmianie prędkości:

1. jeżeli występuje siła od tłumienia T o ośrodek (nie jest to tłumienie wewnątrzmateriałowe w wale i tarczy), to wał obraca się jednorazowo dodatkowo wokół swojej osi o pewien niewielki kąt φ, niezależnie od swoich obrotów z częstością ; zmiana kąta  może wynosić od wartości bliskiej zera do bliskiej, ale mniejszej od π,
2. jeżeli nie ma siły od tłumienia T, to dodatkowy obrót nie występuje i utrzymuje się stabilnie kąt φ = 0 przy zmianie prędkości od małych wartości do wartości krytycznej,
3. jeżeli nie ma siły od tłumienia T, to po przekroczeniu prędkości krytycznej występuje dodatkowy obrót  i utrzymuje się stabilnie kąt φ = π przy zmianie od krytycznej wartości do każdej większej.

Na rysunku 4 jest przedstawiona schematycznie masowa tarcza wirująca bez tarcia o otoczenie.

Skokowy obrót następuje w rezonansie czyli wtedy, gdy częstość wynikająca z obrotów wirnika  uzyska częstość własną .

Z rysunku 4 odczytujemy, że przy braku tłumienia o zewnętrzny ośrodek, gięcie wału  przed rezonansem wynika z właściwości mechanicznych układu i kąt  ale po rezonansie jest równe mimośrodowi  przy kącie wyprzedzenia ruchu przez siłę .

Rys. 4. Zachowanie się tarczy bez tłumienia przed i po rezonansie.

Na rysunku 5 jest przedstawiony rozkład sił na masowej tarczy wirującej w ośrodku stawiającym opór w postaci tarcia wiskotycznego.

Rys. 5. Rozkład sił na tarczy o promieniu wirującej w lepkim ośrodku.

Kierunki i wartości tych sił zmieniają się wraz ze zmianą obrotów. Oczywista jest zmiana siły tarcia o otoczenie. Skutkuje ona zmianą obu składowych ugięcia. Ale, niezależnie od współczynnika tarcia i od ilości obrotów, które wirnik wykonuje na minutę, zawsze zachodzą równowagi: składowa siły bezwładności, działająca w kierunku siły tarcia, jest w równowadze z siłą tarcia i składowa siły bezwładności, działająca w kierunku sumarycznego ugięcia, jest w równowadze z siłą sprężystości, działającą w ugiętym wale. Taki mechanizm umożliwia (albo powoduje) to, że powyżej rezonansu i wraz ze zwiększaniem obrotów - amplituda ugięcia wału zbliża się do mimośrodu tarczy e.

Dla dodatkowego zobrazowania „kątowego ustawiania się wirnika” przy precesji prostej, synchronicznej zamieszczono poniższy rysunek 6. Jest to uzupełnienie rysunku 4 w tym sensie, że przedstawia kątowe ustawianie się tarczy w obecności sił tarcia o otoczenie dla różnych, rosnących prędkości obrotowych.

Są na nim przedstawione, w świetle lampy stroboskopowej błyskającej jeden raz na obrót, położenia pojedynczego obciążnika o masie m zamocowanego na promieniu do masowego wałka, mającego podatność na zginanie El przy zwiększającej się prędkości obrotowej w obecności tarcia (tłumienia) o otoczenie.

Z rysunku można odczytać:

1. wraz ze wzrastającą prędkością obrotową rośnie kąt względnego obrotu wału , skutkujący zamianą tworzącej walca wału, która jest np. maksymalnie rozciągana, na inną i przez to wyprzedzeniem o ten sam kąt miejsca posadowienia obciążnika o masie m które jest oddalone od środka wału o e; kąt jest mierzony w kierunku obrotów od linii ugięcia geometrycznego wału znajdującego się w punkcie D, aż do osiągnięcia (asymptotycznie) wartości przy nieskończenie dużej prędkości obrotowej;
2. dla prędkości obrotowej zdecydowanie przekraczającej prędkość rezonansową obciążnik zbliża się do rzeczywistej osi wirowania, okrążając punkt zamocowania do podatnego wału;
3. maksymalne ugięcie wału następuje po „nieznacznym” przekroczeniu kąta wyprzedzenia wynoszącego 90°.
    

Rys. 6. Zachowanie się niewyważonego wału podatnego na zginanie przy zwiększającej się prędkości obrotowej.

Powyższy przykład obrazuje jedną z najistotniejszych cech wirników w ruchu. Jest nią tzw. samocentrowanie. Dzięki występowaniu procesu samocentrowania, w trakcie np. zwiększania prędkości obrotowej, podatny i ugięty wirnik przyjmuje różne postaci własne ugięcia. Obecnie stwierdzamy tylko, że wskutek jego działania wirniki trójwymiarowe przyjmują postaci własne ugięć. Poszczególne postaci pojawiają się przy konkretnych prędkościach obrotowych. Prześledźmy mechanizm powstawania kolejnych postaci ugięcia, począwszy od pierwszej postaci.

Przy zwiększaniu prędkości obrotowej wirnik ugina się tak jak wirująca dziecięca skakanka. Oś geometryczna przyjmuje kształt połowy sinusoidy. Jej środek krzywizny leży po przeciwnej stronie osi geometrycznej w stosunku do kierunku ugięcia. Przy kolejnym zwiększeniu prędkości obrotowej, począwszy od jednego z końców wirnika (tego, który jest bardziej podatny giętnie lub obciążony miejscowym momentem), mechanizm samocentrowania powoduje takie przegięcie wirnika, że nowo powstający miejscowy środek krzywizny jest przesunięty kątowo o  w stosunku do poprzedniego. Leży po przeciwnej stronie rzeczywistej osi wirowania. Przy wzroście prędkości obrotowej nowe przegięcie się powiększa - aż do uzyskania ugięcia w kształcie całej sinusoidy. Tak powstaje druga postać modalna. Przy kolejnym wzroście prędkości obrotowej znowu, na jednym z końców wirnika, powstaje kolejne przegięcie, które ma środek krzywizny po przeciwnej stronie w stosunku do aktualnie występującego. Tak powstaje trzecia postać modalna ugięcia.

Wirnik w postaci regularnego wałka o średnicy  można podzielić na nieskończenie wiele cienkich tarcz, ułożonych jedna za drugą i utrzymywanych względem siebie za pomocą sił sprężystości. Wartość tych sił rośnie wraz z wzajemnym poprzecznym przemieszczeniem się dwóch, sąsiadujących ze sobą, tarcz. W ogólności tarcze mogą się dowolnie układać. Przy takich założeniach może powstać nieskończenie wiele różnych postaci własnych ugięć. Na poniższym rysunku, dla uproszczenia, wirnik składa się z trzech tarcz. W wyniku tego mogą powstać trzy różne kombinacje wzajemnych przesunięć. Dla trzytarczowego wirnika powstają więc trzy postaci własne ugięcia.

Rys. 7. Postaci własne wału gibkiego.

Pierwsza postać powstanie, gdy wszystkie tarcze przemieszczą się w jednym kierunku. Druga, gdy środkowa pozostanie w spoczynku, a zewnętrzne przemieszczą się w przeciwnych kierunkach. Trzecia, gdy kolejne tarcze przemieszczą się w różnych kierunkach.

Przeanalizujmy, jakie warunki musi spełnić obciążenie zewnętrzne, czyli niewyważenie, żeby ujawniła się konkretna kombinacja. Sprawdźmy zachowanie się bezmasowego sprężystego wału, na którym są zamocowane trzy tarcze mające masę. Układ ma więc trzy stopnie swobody.

Prawdziwe są spostrzeżenia dotyczące zachowania się takiego układu:

1. Gdy na bezmasowym, podatnym na zginanie wale, zamocujemy trzy masowe tarcze, które będą kolejno obciążone, w jednej płaszczyźnie zawierającej oś obrotu, niewyważeniem o wartościach równych rzędnej funkcji 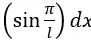 w miejscach zamocowania tarcz, wzdłuż długości wału, to zostanie wymuszone dominujące ugięcie według pierwszej postaci własnej przy jednej, wybranej prędkości obrotowej. Przy innych prędkościach ugięcia wystąpią, ale nie będą dominujące.
2. Gdy na bezmasowym, podatnym na zginanie wale, zamocujemy trzy masowe tarcze, które będą kolejno obciążone niewyważeniem o wartościach, równych rzędnej funkcji 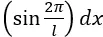 w miejscach zamocowania tarcz, wzdłuż długości wału, to zostanie wymuszone dominujące ugięcie tylko według drugiej postaci własnej przy wybranej, ale innej prędkości obrotowej. Przy innych prędkościach ugięcia wystąpią, lecz nie będą dominujące.
3. Gdy na bezmasowym, podatnym na zginanie wale, zamocujemy trzy masowe tarcze, z których tylko jedna będzie obciążona niewyważeniem o wartości niedopasowanej do rzędnej funkcji sinus w miejscu jej wystąpienia, wzdłuż długości wału, to zostaną wymuszone ugięcia wszystkich tarcz według wszystkich możliwych postaci własnych, ujawniające się przy prędkościach wybranych w punktach: i  - pod warunkiem, że „niedopasowana” tarcza nie jest posadowiona w węźle jednej z postaci.

Należy teraz dopisać czwarty punkt.

4. Gdy na bezmasowym, podatnym na zginanie wale zamocujemy „nieskończoną” ilość masowych tarcz, które będą tak obciążone niewyważeniem, że stosunki tych niewyważeń będą równe stosunkom amplitud funkcji 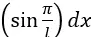 odpowiednio w miejscach zamocowania poszczególnych tarcz, wzdłuż długości wału, to zostanie wymuszone ugięcie tylko według pierwszej postaci własnej przy jednej prędkości obrotowej, dopasowanej do sztywności wału i ilości wirującej masy. Przy innych prędkościach jakiekolwiek ugięcie nie wystąpi.
    

Zwróćmy uwagę, że punkty 4 i 1 są ze sobą powiązane liczbą tarcz.

Zastanówmy się, dlaczego wirująca dziecięca skakanka, uginając się, przyjmuje kształt połowy czystej sinusoidy i nie zawiera innych składowych ugięcia?

Zauważamy, że przyjmuje pierwszą postać własną ugięcia wirnika podatnego. Robi tak dlatego, że są spełnione warunki zawarte w 4. punkcie. Nie tylko w kilku wybranych punktach ale każdy elementarny odcinek „wirnika” jest obciążony niewyważeniem o wartości dopasowanej do miejsca, które zajmuje wzdłuż długości, według funkcji . Każdy elementarny odcinek skakanki ma tę samą masę. Dopasowanie niewyważenia do miejsca występowania odcinka „wirnika” następuje poprzez oddalenie się tego odcinka od osi wirowania.

Niewyważenie ma więc postać: .

Ta sama zasada obowiązuje dla kolejnych postaci ugięć (np. dla  ).

Ma to znaczenie w praktyce wyważania. Ze względu na ograniczony dostęp do powierzchni wirnika podatnego korekcję wykonuje się w kilku wybranych punktach. Już to ograniczenie jest źródłem powstawania kolejnych ugięć wirnika w pozostałych postaciach. Dodatkową przyczyną małej skuteczności wyważania może być niewłaściwy dobór miejsc korekcji. Bywa, że nie są one optymalnie położone wzdłuż długości wirnika i, minimalizując aktualnie wyważane ugięcie, są źródłem kształtowania się innych postaci.

Masowy wirnik, w kształcie regularnego wału, mając ciągły rozkład masy wzdłuż długości, ma teoretycznie nieskończoną ilość stopni swobody.

Załóżmy, że wirnik jest obciążony niewyważeniem skupionym, w poszczególnych punktach,  dowolnie rozrzuconym wzdłuż długości i na różnych kątach. Jest on dodatkowo wstępnie nieregularnie ugięty. Ma więc wszystkie składowe niewyważenia, które mogą wejść w kolejne rezonanse.  Jak zachowa się taki wirnik posadowiony na wyważarce podkrytycznej? Przy zwiększaniu prędkości obrotowej wskazy wektorowe, zainstalowane na ekranie wyważarki, pokażą wzrosty i zmiany kierunków działania sił obciążających podpory. Wzrosty zakończą się prawie wspólnym kierunkiem działania i dużymi amplitudami w pobliżu pierwszego rezonansu. Charakterystycznym jest także wyraźny obrót wektorów, przy niewielkiej zmianie prędkości obrotowej w pobliżu częstości rezonansowej - zarówno poniżej, jak i powyżej rezonansu. Wynika to z niewielkiego tarcia towarzyszącego obrotom, w obecności przygotowania się wirnika do kolejnej postaci ugięcia. Zwiększenie prędkości obrotowej w pobliże drugiej częstości rezonansowej spowoduje wyraźny obrót, w pierwszej kolejności, jednego ze wskazów (wektorów), a następnie drugiego tak, że oba znajdą się na kątach różniących się między sobą o . Powstanie druga postać ugięcia. Ustalenie się obu kątów zależy od kątowego położenia na wirniku składowej momentowej niewyważenia. Nie ma innej zasady, co do kątowego ustalenia się kolejnych postaci ugięcia, niż ta, według której położenia kątowe kolejnych postaci zależą od rozkładu pierwotnego niewyważenia (lub aktualnego, jeżeli po każdym etapie następuje doważanie). Ustalenie się trzeciej postaci nastąpi po obrocie obu wskazów tak, że znowu przyjmą ten sam kierunek.

Wyważarki stacjonarne i aparatura do wyważania w łożyskach własnych, produkowane przez Przedsiębiorstwo CIMAT Sp. z o.o. z Bydgoszczy, umożliwiają taki rodzaj wyważania.

Podsumowanie:

1. Podatny na zginanie wirnik, ugięty w trakcie obrotów, nie wykonuje drgań, lecz ruch precesji prostej i synchronicznej. Nie przegina się jeden raz na obrót. Przy wybranej prędkości obrotowej tworzące walca wirnika dzielą się na niezmiennie rozciągane i niezmiennie ściskane.
2. W obecności sił tarcia o otoczenie, przy zmianie prędkości obrotowej, wirnik niezależnie od swoich obrotów wykonuje mały, dodatkowy ruch obrotowy, zgodny z kierunkiem obrotów. Kolejne tworzące rozciągane zaczynają być ściskane, a jeszcze inne rozciągane.
3. Przy rosnącej prędkości obrotowej wirnik ugina się, przyjmując kolejne postaci ugięcia: od połowy sinusoidy do wielokrotności połówek sinusoidy.
4. Położenia kątowe, względem wirnika, każdej z postaci ugięcia zależą od rozkładu pierwotnego niewyważenia na wirniku i innego przesunięcia kątowego, zależnego od nowej wartości tłumienia.
5. Dwie różne siły, oddziałując na wał wirnika, wywołują jego ugięcie, jeżeli jest obciążony niewyważeniem i wiruje w otoczeniu ośrodka o danej lepkości. Są to: siła bezwładności i siła tarcia. Dlatego przy zmianie niewyważenia, nawet bez zmiany obrotów, mogą wystąpić problemy ze zbieżnością wyważania. Wynikają one z dodatkowej zmiany położenia kątowego wirnika w wyniku ustalenia się innego kierunku działania sumarycznego ugięcia . Sumaryczne ma składowe: od siły tarcia  i od siły bezwładności . Zmianie ulega, w tym wypadku, .
6. Poszukanie każdego z tych kątów następuje w osobnej procedurze, związanej kolejno z identyfikacją i kalibracją maszyny. Nie została ona tutaj przedstawiona.
    

Powyższe zagadnienia zostały szczegółowo opisane w mojej książce: M. Malec: Wyważanie dynamiczne wirników w teorii i praktyce. Bydgoszcz 2022.

Dystrybutorem książki jest: www.fachowa.pl